Puisqu’il est question de musique en ce dimanche, voici un article passionnant lu sur le site de Kulturica : Pythagore et la musique.

Kulturica est un site dédié à la culture classique : musique classique, littératures du monde, beaux-arts, mathématiques – arithmétique et géométrie – telles que les concevaient les Anciens, mythologie grecque. Voici quelques uns des domaines dans lesquels s’est exprimé le génie de l’humanité.

Pont entre les âges et les civilisations, la culture doit être préservée : elle est l’un des plus beaux trésors de l’humanité. La perdre, c’est perdre l’humain en nous. C’est perdre aussi une source intarissable de joie.

Pythagore a mis en évidence les rapports étroits qui unissent la musique et le nombre, rapports que l’on peut résumer aujourd’hui sous le terme de « fréquence ». Et, pour Pythagore, des nombres « harmonieux » entre eux donnent des sons harmonieux entre eux.

L’inexistence des mathématiques musicales avant l’époque de Pythagore, du moins en Occident, n’a jamais empêché personne de jouer de la musique : un roseau percé de trous, une corde tendue pincée à différentes hauteurs, et aussi le chant, les boîtes sur lesquelles on peut battre des rythmes… tout cela existait déjà bien avant les chiffres.

Mais Pythagore fut celui qui relia le nombre à la musique, qui lança l’idée que le fait que deux sons joués ensemble, simultanément ou l’un après l’autre, donnent une impression harmonieuse pouvait s' »expliquer mathématiquement », ou plutôt, que musique et nombre étaient intimement liés et que les lois de l’harmonie de l’un se reflétaient dans l’autre. Et vice versa.

Ses remarques très justes, confirmées par les sciences acoustiques, n’ont malheureusement jamais été comprises ni employées intelligemment en Occident. Au système des « tierces successives » (on expliquait qu’un accord était harmonieux « parce que » il était composé de plusieurs tierces successives), a priori élégant mais qui ne repose sur aucune base acoustique, a succédé l' »atonal », en complet désaccord avec notre système physiologique de perception auditive, ou la recherche du hasard en musique, ce qui nous ramène au « son », puisque ce qui différencie le « son » de la « musique », c’est une notion de cohérence ou d’ordre, sans laquelle l’humain est perdu : le « cosmos » contre le « chaos », ou le geste créateur divin contre le « tohu-bohu », invivable parce qu’impensable.

Seuls les Arabes ont poursuivi les travaux de Pythagore, relayés, entre autres, par Aristote, ce qui a fait de leurs bases musicales (les « maqam », que l’on traduit de manière un peu simpliste par « modes », faute de mieux) les plus raffinées du monde.

Peut-être ce sujet fera-t-il l’objet d’une page particulière du site Kulturica, ou peut-être non, mais il faut introduire ici le concept pythagoricien essentiel de Tetraktys.

« Tetraktys » signifie « à quatre rayons », « au quadruple éclat rayonnant ». Ce mot évoque une lumière rayonnante (« aktys »), et le nombre 4 (« tetra »).

Il existe un symbole pour désigner ce principe. Le voici :

10 points ordonnés en un triangle équilatéral, un point central entouré de 9 points, chaque base du triangle composée de 4 points, quatre rangées des 4 premiers nombres successifs, dont la somme vaut 10… il y a de multiples manières de voir la Tetraktys.

Retenons seulement pour l’instant les chiffres 1, 2, 3 et 4.

Plusieurs traités antiques et médiévaux rapportent cette histoire (ou cette légende) d’un Pythagore surpris et charmé par les sonorités harmonieuses rendues par des marteaux de différents poids frappant sur une enclume. Il pesa les marteaux, et découvrit qu’ils pesaient 6, 8, 9 et 12 (unités de poids). Toutes les associations deux par deux de ces sons produisaient toutes, à l’exception de l’association 8 et 9, des sons harmonieux.

Rapportons ces chiffres à 6, et nous obtenons les fractions suivantes (réduction en facteurs premiers) :

qui sont respectivement que que l’on nomme l’unisson, la quarte, la quinte et l’octave. Et nous retrouvons dans ces chiffres les composants de la Tetraktys.

Ajoutons que cette histoire est plutôt une légende, car les « harmonies » ne sont pas proportionnelles au poids, mais à leur racine carrée. L’expérience de Pythagore est purement symbolique. D’ailleurs, il se consacrera par la suite uniquement aux sonorités des instruments à cordes.

Un son est une vibration de l’air qui vient exciter notre tympan. Et une vibration se définit par son amplitude (le son est-il fort ou faible ?) et sa « fréquence » ou nombre de vibrations par unité de temps (l’unité commode dans le domaine des sons audibles est la seconde) : des fréquences élevées vont produire des sons aigus, et des fréquences faibles, des sons graves. Sur la corde d’une guitare, d’un luth, d’un violon…, plus la corde est courte, plus la fréquence est élevée. Dans les faits, la fréquence est inversement proportionnelle à la longueur de corde.

Si l’on prend deux sons de fréquences différentes, on peut définir les rapport des fréquences entre les deux, et les réduire en facteurs premiers entre eux (les simplifier) : plus la fraction sera simple, plus les deux sons seront harmonieux entre eux.

Si ce rapport de fréquence est assez proche d’une fraction simple, le cerveau se « recalera » sur le rapport harmonieux, mais, a contrario, si la différence est juste un petit peu trop importante, le son paraîtra très discordant, avec apparition d’un phénomène de battement (on entend une variation du volume sonore répétitive et très régulière, comme une « onde » qui « envelopperait » les deux sons joués ensemble).

Le rapport de 2 à 1 (une corde de longueur deux fois plus petite que la corde de base, ou plus simplement une corde pincée en son milieu) donnera le son le plus harmonieux. C’est ce que l’on appelle en musique l’octave. Et les deux sons espacés d’une octave sont tellement harmonieux entre eux qu’on les nomme du même nom : on pourrait très bien nommer de noms différents absolument toutes les notes (88 noms différents pour les notes du piano, auxquelles il faudrait ajouter les noms des notes noires, qui en portent chacune deux – c’est pourtant ce que font traditionnellement les musiciens arabes « savants », qui nomment chaque note d’un nom différent, mais seulement sur deux octaves ; il y a quand même 24 notes différentes par octave).

3/2 est la fraction la plus simple juste après 2/1, et ensuite vient 4/3. Nous retrouvons les 4 marteaux du forgeron, et aussi les quatre chiffres, associés deux par deux, de la Tetraktys.

Sur une corde de luth (nous prendrons comme exemple le luth, parce que c’est en quelque sorte une guitare sans frettes, qui laisse entière liberté au musicien pour régler sa hauteur de son), on retrouve ces notes en pinçant une corde respectivement au tiers de la hauteur (les deux-tiers de la corde vibrent, rappelons-nous que fréquence et longueur de corde sont inversement proportionnels) et au quart de la hauteur (les 3/4 de la corde vibrent).

Alors il devient facile, sur un luth à plusieurs cordes, d’accorder chaque corde à la fréquence 3/2 de la précédente (ici, on n’accorde pas par les longueurs, mais par l’épaisseur de corde et par sa tension).

Pourquoi 7 notes ? C’est pourtant si simple ! C’est parce que nous avons 5 doigts à chaque main !

Prenons notre luth en mains, accordé en fréquences successives « 3/2 ». On applique le pouce derrière le manche, pour le tenir, on joue la corde à vide (« DO »), on applique l’index (« RÉ »), le majeur (« MI »), l’auriculaire (« FA »). On jouerait bien avec le petit doigt, mais il n’est pas très fort et en obtenir un son net n’est pas très naturel (bien sûr, nos virtuoses actuels en sont parfaitement capables, mais nous parlons ici de musique au quotidien). Alors, pour aller plus haut, nous prenons la corde suivante, « SOL » à vide, « LA » à l’index, « SI » au majeur, et nous revenons à « DO » avec l’auriculaire. Ce qui fait bien 7 notes par octave (nous ne comptons bien sûr le « DO » qu’une seule fois).

Ainsi, on joue 4 notes sur la même corde, ce qui nous a donné le terme de « tétracorde ». C’est une notion tout à fait naturelle, mais qui n’a plus beaucoup de sens aujourd’hui.

Cette explication, qui n’a pourtant jamais été exposée à notre connaissance dans un contexte de musique occidentale, nous paraît claire et simple.

Note système musical actuel est un système « à tempéraments égaux » : c’est-à-dire qu’il est basé sur les éléments posés par Pythagore (l’octave, les sept notes…), mais il a été déformé pour des raisons techniques, essentiellement pour la commodité des instruments à clavier, qui se sont imposés dans la musique occidentale comme les instruments de référence (orgue pour la musique religieuse, clavecin puis piano pour la musique profane). Il fallait bien fixer à une hauteur précise et invariable les « notes noires ». Nous verrons plus précisément ce que cela signifie, mais il faut savoir que toutes les « finesses » que nous allons rencontrer dans le système pythagoricien ont été très largement simplifiées dans le système musical actuel.

Le système pythagoricien est tellement fort, tellement cohérent « mathématiquement », que, quel que soit le bout par lequel on le prenne, nous retombons toujours sur nos pieds.

En théorie musicale, on donne le nom de « cycle des quintes » à ce système. Platon, dans son Timée, arrive exactement au même résultat par des calculs de moyennes. Et l’on peut également utiliser seulement les quatre notes 1, 4/3, 3/2 et 2, en se basant sur la Tetraktys.

Pour la commodité du raisonnement, on va nommer les 4 notes DO, FA, SOL et DO aigu.

Regardons le graphique ci-dessous : entre DO et FA, l’intervalle de fréquence (qui se calcule non par soustraction mais par division) est de 4/3. C’est le même intervalle qui sépare le SOL du DO aigu : 2 / (3/2) = 4/3.

Entre FA et SOL, ce fameux intervalle dissonant dont nous parlait Pythagore est de 9/8. Cet intervalle est très commode : nous allons pouvoir définir la hauteur des « doigts » sur chacune des cordes à l’aide de cet intervalle. Et cela ne va pas tomber juste, mais pas très loin.

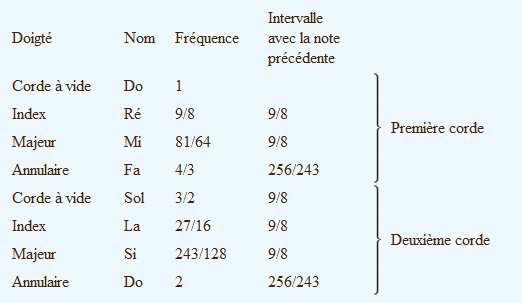
Le problème, c’est que l’intervalle de 9/8 (1,125) « mange » un tout petit peu trop les intervalles de DO à FA et de SOL à DO aigu, ce qui fait qu’il ne reste plus que 256/243 (1,0535…) pour les intervalles de MI à FA et de SI à DO. On nomme l’intervalle de 9/8 le « ton » et l’intervalle de 256/243 le « demi-ton », qui n’est pas exactement la moitié d’un ton. Il est un tout petit peu plus petit, c’est ce que l’on nomme en musique occidentale le « demi-ton diatonique ». Le « reste » est un autre « demi-ton », 2187/2048, dit « demi-ton chromatique », qui est le complément de 256/243 pour arriver au ton.

Ce n’est pas un problème, en tout cas, pour l’expression musicale, qui se trouve enrichie de toutes ces possibilités qu’offre le choix entre un intervalle « complet », « franc » et un intervalle plus petit, plus subtil, plus sensible…

Le Dialogue de Platon connu sous le titre de Timée est l’un des favoris des amateurs de mystères : on y parle de l’Atlantide et de la création du monde. On y parle aussi d’un Dieu unique et créateur, dans une Grèce polythéiste…

Mais on y parle aussi de musique, d’une manière fort étrange :

Platon nous entraine dans une description de la création du monde à partir d’un « mélange » du « Même », de l' »Autre » et d’un troisième terme qu’il nomme « Réalité ». De ce mélange, le Créateur prélève des parts dans certaines proportions qui se révèlent être… des notes de musique !

Les premières « fréquences » prélevées sont, dans l’ordre donné par Platon : 1, 2, 3, 4, 9, 8, 27.

27 étant compris entre 16 et 32, Platon nous invite à définir les notes sur plus de 4 octaves.

Il comble ensuite les intervalles doubles (1, 2, 4, 8) et triples (1, 3, 9, 27) par de « nouveaux prélèvements » calculés comme leurs moyennes arithmétiques (la moitié de la somme des deux termes, le « milieu » en quelque sorte) et harmonique (si l’on nomme m la moyenne, et a et b les deux extrêmes, on a l’égalité (m-a)/a = (b-m)/b ; il s’agit de la moyenne arithmétique pour les inverses : l’inverse de m est la moyenne arithmétique de l’inverse de a et de l’inverse de b).

Ainsi, pour l’intervalle de 1 à 2, la moyenne arithmétique est de 3/2 et la moyenne harmonique de 4/3 (cela nous rappelle quelque chose).

De 2 à 4 : 3 et 8/3

De 4 à 8 : 6 et 16/3

De 1 à 3 : 2 et 3/2 (rien de nouveau)

De 3 à 9 : 6 et 9/2

De 9 à 27 : 18 et 27/2

Résumons tout cela dans le tableau suivant :

Les fréquences, d’après le Timée de Platon

Nous avons ajouter sous les fréquences les notes auxquelles elles correspondent dans notre système.

Ainsi, après DO, FA et SOL, apparaissent LA et RÉ. Ces 5 notes sont celles qui composent les gammes d’Afrique sub-saharienne et d’Extrême-Orient, les systèmes dits « pentatoniques ».

Platon parle ensuite des intervalles de 4/3 qu’il faut combler au moyen de l’intervalle de 9/8, comme précédemment, et qu’il apparaît des intervalles de 256/243. On définit ainsi les MI et SI.

Dans le traités de théorie musicale actuels, on parle du système pythagoricien comme issu du « cycle des quintes ». Qu’est-ce que cela signifie ?

D’un point de vue strictement logique, il faudrait parler de « cycles croisés des octaves et des quintes ». Le « cycle des quintes » s’appuie sur deux faits :

– que l’on « assimile » entre elles les notes espacées d’octaves (tous les « DO », tous les « RÉ »…)

– que toutes les notes peuvent être définies comme la « quinte d’une quinte d’une quinte… » d’une note de base, vers l’aigu ou vers le grave.

Ainsi, le « RÉ » est la quinte de « SOL » (rapport 3/2 entre les fréquences des deux notes), qui est la quinte de « DO », et inversement, « DO » est la quinte de « FA ». Voici ce « cycle des quintes » :

Or, si l’on continue ce jeu de part et d’autre des 7 notes de la gamme, on découvre les « notes noires » du piano, ou notes altérées.

Par exemple, la quinte au dessus de SI est une note plus haute que FA mais plus basse que SOL, c’est le FA # (dièse), dont l’écart avec le FA est exactement de 2187/2048. De l’autre côté, la note dont FA est la quinte est un SI b (bémol), plus bas que le SI « naturel » d’un rapport de fréquences de 2187/2048. Et l’on définit ainsi les notes »diésées » et « bémolisées ». Ce ‘2187/2048’, nous l’avons déjà vu : c’est l’autre moitié du ton, la première moitié étant le demi-ton de 256/243. Celui-ci, qui sépare deux notes de noms différents, comme « MI FA » et « SI et DO », est nommé demi-ton diatonique (« dia », comme dans « division », signifie « séparation », et se retrouve également dans le mot « diable », celui qui divise). Et l’autre demi-ton, de 2187/2048, qui sépare des notes de même nom (FA et FA#, Si et SIb), est nommé « chromatique », de « chroma » en grec qui signifie « couleur », parce qu’il change la « couleur » de la note.

Là où le bât blesse, c’est que nous n’avons pas réellement un cycle : si nous continuons à le parcourir, nous arrivons au MI# qui est proche, certes, du FA, mais qui n’en est pas identique, et la différence est audible. Elle est exactement de 531441/524288. On nomme cet intervalle « comma pythagoricien ».

Si la plupart des traditions musicales ont bien vécu avec ce comma, ce n’est pas le cas de la musique occidentale qui a vécu ce « comma » comme une malédiction, et ce qui l’a conduit à la gamme à tempérament égal que l’on connaît aujourd’hui, composée de 12 demi-tons égaux. Il n’y a plus de différence entre un FA fièse et un SOL bémol, ils sont joués par la même note au piano. Pas de différence « théorique », car, en fait, lorsqu’on les laisse seules, les cordes (dans un quatuor à cordes, par exemple) retrouvent très vite des liberté vis à vis du système tempéré, ce qui donne des couleurs particulières, nettement audibles dans les accords.

Ces 12 demi-tons sont égaux à exactement « racine douzième de 2 », et c’est un nombre « réel », comme pi, par exemple, qui ne peut être écrit sous forme de fraction.

Mais fixer ainsi de manière rigide la hauteur des notes réduit à néant les possibilités de « coloration » de ces même notes, et, par là même, le pouvoir d’émotion de la musique. La musique occidentale s’est ainsi naturellement tournée (et cette évolution s’est faite au fur et à mesure que l’on tournait le dos, via divers tempéraments, au système pythagoricien) vers l’harmonie, ou la manière de « colorer une note » par d’autres notes jouées simultanément, la virtuosité des interprètes (notamment au piano, où 10 doigts sont parfois à peine suffisants pour jouer certaines partitions tant il y a de notes à jouer en même temps), la multiplication et la variété des instruments et l’enrichissement de leur timbre.

Le « cycle des quintes » est une manière assez imagée de décrire un phénomène mathématique simple : pour pouvoir chiffrer assez finement des fréquences qui allaient se multiplier et se diviser entre elles, il fallait des facteurs de base aussi petits que possible. On a donc pris les plus petits entiers possibles : 2 et 3. Les numérateurs et les dénominateurs de toutes ces fractions sont, par construction, des puissances de 2 et de 3. Et si le cycle des quintes ne peut être un cycle « fermé », c’est que les puissances de deux et de trois sont par définition des facteurs irréductibles et que jamais, même en continuant sur un nombre incalculable de cycles, nous ne retomberons sur des nombres entiers.

Reprenons les calculs tirés de Platon : après DO, SOL et FA, les notes RÉ et LA sont fixées, à des hauteurs respectives de 9/8 et de 27/16. C’est, rappelons-le, le système pentatonique. Quant à MI et SI, on pourrait tout aussi bien les définir comme un ton au dessus de RÉ et LA que comme un ton en dessous de FA et DO, ce qui les définit comme nos actuels MI bémol et SI bémol. La notation allemande nous enseigne que la note la plus employée était SI bémol, notée par la lettre B, alors que le SI naturel est noté H.

Alors, un MI à 81/64 (le mi naturel) ou un MI à 32/27 (le mi bémol) ? Un SI à 243/128 (le si naturel) ou à 16/9 (le si bémol) ? Il faut avouer que les fractions relatives aux MI et SI bémolisés sont bien plus simples !

Mais les traditions musicales arabo-musulmanes (traditions arabes proprement dites, persane et turque…) vont encore plus loin et définissent encore une autre hauteur pour ces notes, une hauteur « intermédiaire » entre le MI et le MI bémol, entre le SI et le SI bémol, une sorte de « trois-quart de ton », séparant en deux parts à peu près égales ce grand intervalle séparant RÉ de FA et LA de DO (intervalle de 32/27). Mais il n’est pas possible de donner pour cet intervalle de « 3/4 de ton environ » une fraction relativement de puissances de 2 et de 3. L’assimilation de cet intervalle à une fraction simple conduit à utiliser d’autres nombres entiers comme numérateurs et dénominateurs, mais cela, c’est une autre histoire…

Confirmation de cette « instabilité » propre à MI et SI dans la musique arabe : ce sont ces deux notes (sauf exceptions rares) qui portent ce « quart de ton » ou « demi-bémol ».

En conclusion, nous avons voulu faire sentir à quel point des évidences (7 notes, « identité » de deux notes séparées par une octave…) ne le sont pas, mais que, a contrario, des notions, des termes, des définitions qui nous semblent aujourd’hui étranges (tétracorde, comma…) prennent appui sur des réalités concrètes que notre musique, après des siècles de pratique, a presque totalement oubliés : il n’en reste plus que des notions fort abstraites et qui sont totalement inutiles aux compositeurs comme aux interprètes. Nous avons voulu également retrouver une base commune qui permettrait aux musiciens du monde entier d’échanger et de se comprendre.

A lire, entre autre, sur le même site, la section Pythagora :

– Autour de Pythagore : La vie de Pythagore • Le théorème de Pythagore • Pythagore et la musique
– Autour du théorème de Pythagore : Un triangle remarquable • Le jeu chinois du tangram • Le tracé du pentagramme • La suite de Fibonacci • La leçon de géométrie de Socrate • Les proportions des pyramides d’Égypte • Les cinq solides platoniciens

anti